背景:MicroPython上で動かせる軽量FFTライブラリを作りたい
課題:微積・三角関数→フーリエ級数→フーリエ変換→離散フーリエ変換と積み上げて理解したかったけど、フーリエ変換→離散フーリエ変換の間がどうにも埋まらない
取り組み:途中の証明をすっ飛ばして、離散フーリエ変換(DFT)の公式ありきで、実装する
結論:愚直実装版だがDFTは動いた(サンプル数8でテスト)
詳細:
これまで式を追いかけてなんとかDFT/FFTを理解したいと思ってきたが、フーリエ変換と離散フーリエ変換(DFT)の間はかなりの思考過程を経る必要があるように思えてこの間のギャップが埋まらない。世の中の記事や資料には、離散フーリエ変換(DFT)の公式からソフトウエア実装を説明する記事は結構あるので、式を追いかけて理解するのは一旦やめて、公式ありき*1で実装してみる。DFTを実装して動作確認したら、次は計算量を減らすためのバタフライ演算を導入して、FFTになると思う。一旦FFTは置いといて、愚直に2重ループを回すDFTをPython等で実装してみる。
参考資料をいろいろ見ていると、DFTの公式としては以下
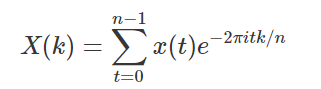
eの-2πitk/nはsin/cosで表現すると、cos(2 * pie * t * k / n) + i * sin(- 2 * pie * t * k / n )
これをサンプル実装すると以下のような2重ループになると。
for (k = 0; k < N; k++) { // k倍の周波数を計算
X.real = 0; // 実数部
X.imag = 0; // 虚数部
for (t = 0; t < N; t++) { // Nサンプル分を加算
angle = 2.0 * Pie * t * k / n ;
X.real += x[t].real * cos(angle) + x[t].imag * sin(angle); // 複素数の実数部計算
X.imag += x[t].imag * cos(angle) - x[t].real * sin(angle); // 複素数の虚数部計算
}
save(X);
}
>>> angle = complex(1,2) >>> angle (1+2j) >>> angle.real 1.0 >>> angle.imag 2.0
import math
def DFT(x, k):
n = len(x)
for k in range(n): # calc each freq
sum_real = 0 # real number of sum
sum_imag = 0 # imaginary number of sum
for t in range(n): # sum for N samples
angle = 2.0 * math.pi * t * k / n
sum_real += x[t].real * math.cos(angle) + x[t].imag * math.sin(angle)
sum_imag += x[t].imag * math.cos(angle) - x[t].real * math.sin(angle)
sum = complex(sum_real, sum_imag)
print(k, sum)
本のサンプルデータを使ってテスト
#!/usr/bin/python3
import math
def DFT(x, k):
output = []
n = len(x)
for k in range(n): # calc each freq
sum_real = 0 # real number part of sum
sum_imag = 0 # imaginary number part of sum
for t in range(n): # sum for samples (N)
angle = 2.0 * math.pi * t * k / n
sum_real += x[t].real * math.cos(angle) + x[t].imag * math.sin(angle)
sum_imag += x[t].imag * math.cos(angle) - x[t].real * math.sin(angle)
output.append(complex(sum_real, sum_imag))
return output
#
# test
#
# set sampling data
x = [0j] * 4
x[0] = complex(1,0)
x[1] = complex(1,0)
x[2] = complex(-1,0)
x[3] = complex(-1,0)
print("*** input data ***")
for data in x:
print(data)
# confert DFT
out = DFT(x, 4)
print("*** DFT output ***")
for k in range(len(out)):
print(k, out[k], abs(out[k]))実行結果(本の説明とは合っているが。。)
$ ./dft.py *** input data *** (1+0j) (1+0j) (-1+0j) (-1+0j) *** DFT output *** 0 0j 0.0 1 (2-2j) 2.8284271247461903 2 0j 0.0 3 (1.9999999999999993+2.0000000000000004j) 2.82842712474619
周期1のSin波の場合
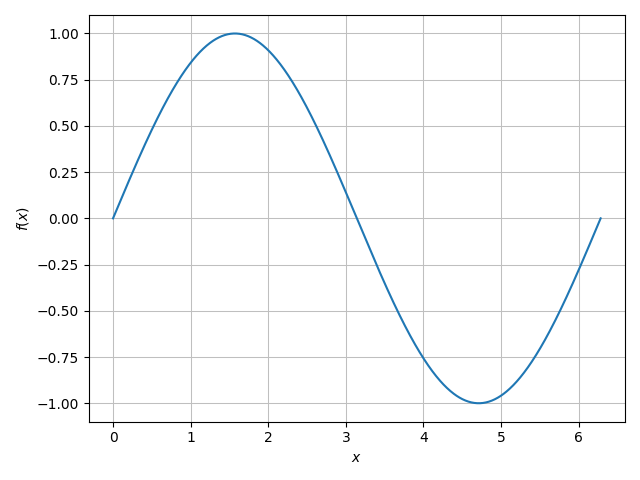
samples = 8
x = [0j] * samples
for i in range(samples):
x[i] = complex(math.sin(math.pi * 2 * i / samples),0)
# confert DFT
out = DFT(x, samples)
print("*** DFT output ***")
for k in range(len(out)):
print(k, out[k], abs(out[k]))実行結果、1倍の周波数で絶対値4と検出(複素数の虚数部が4)*3
$ ./dft.py *** DFT output *** 0 (-2.220446049250313e-16+0j) 2.220446049250313e-16 1 (3.3306690738754696e-16-4j) 4.0 2 (8.104001475739143e-17+1.1102230246251565e-16j) 1.3745339441409415e-16 3 (5.551115123125783e-17-7.771561172376096e-16j) 7.791361360319881e-16 4 (2.220446049250313e-16+2.029061253294536e-16j) 3.007901299453244e-16 5 (1.3877787807814457e-15+1.7763568394002505e-15j) 2.2541902238434278e-15 6 (2.567266157150065e-15+8.881784197001252e-16j) 2.7165633485838455e-15 7 (-3.3861802251067274e-15+3.999999999999999j) 3.999999999999999
sin(Θ) + sin(3Θ)の場合、
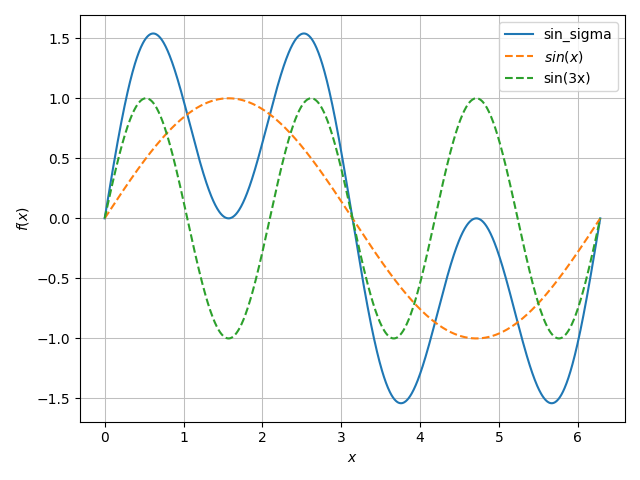
1倍の周波数と3倍の周波数で絶対値4と検出(複素数の虚数部が4)
*** DFT output *** 0 (-8.881784197001252e-16+0j) 8.881784197001252e-16 1 (4.440892098500626e-16-4j) 4.0 2 (4.898587196589412e-16+4.440892098500626e-16j) 6.611934599881869e-16 3 (7.771561172376096e-16-4.000000000000002j) 4.000000000000002 4 (1.7763568394002505e-15+1.3855296899767904e-15j) 2.2528062816609927e-15 5 (-4.440892098500626e-15+4.0000000000000036j) 4.0000000000000036 6 (5.5141545874470235e-15-4.440892098500626e-16j) 5.5320083189171275e-15 7 (-6.328271240363392e-15+3.9999999999999987j) 3.9999999999999987
とまぁここまではそうとして、、元波形がcosの場合は??実数部分で検知?
cos(Θ) + cos(3Θ)の場合...
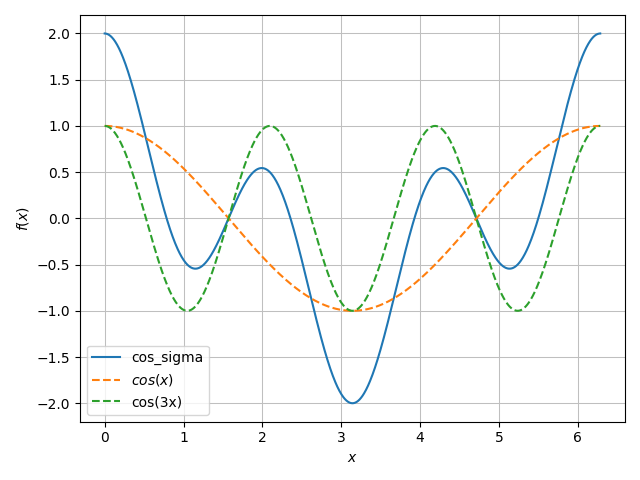
以下のように1倍周波数と3倍周波数の実数部分で検知されている。。なるほど。
*** DFT output *** 0 (-7.428289848809505e-16+0j) 7.428289848809505e-16 1 (4.000000000000001-2.857720186560418e-16j) 4.000000000000001 2 (-3.6739403974420633e-16+7.313866074287308e-16j) 8.184770919003633e-16 3 (3.999999999999999-7.756307383149842e-16j) 3.999999999999999 4 (1.0335278545193e-15-9.79717439317882e-16j) 1.424087808729102e-15 5 (3.999999999999999+2.7350656169507486e-15j) 3.999999999999999 6 (-3.67394039744203e-16-2.6908214860644963e-15j) 2.715786930211188e-15 7 (4.000000000000001+2.2452068972918088e-15j) 4.000000000000001
位相ずれは、実数部と虚数部の比率が変わると。。。
sin(Θ + π/4 ) + sin(3Θ)の場合
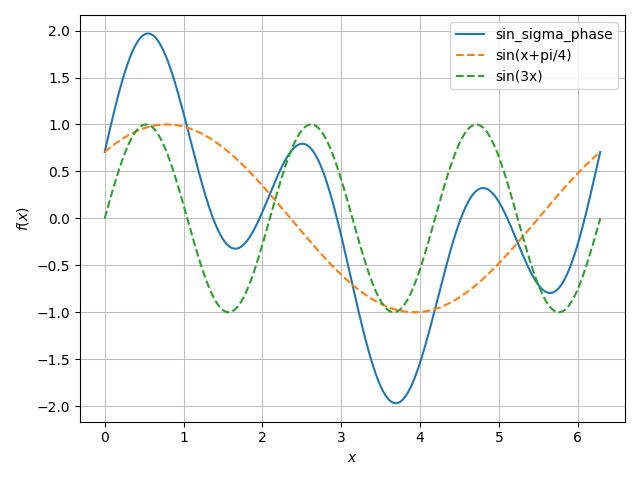
以下の通り、1倍の周波数の実数部と虚数部で、同じ比率になっている。2√2か。。なるほど。。
*** DFT output *** 0 (-1.1102230246251565e-15+0j) 1.1102230246251565e-15 1 (2.8284271247461903-2.828427124746191j) 4.000000000000001 2 (2.4757346845116496e-16+1.1102230246251565e-16j) 2.713274293635243e-16 3 (9.43689570931383e-16-4.000000000000002j) 4.000000000000002 4 (1.5543122344752192e-15+9.797174393178836e-16j) 1.837316734573258e-15 5 (-3.2751579226442118e-15+4.000000000000003j) 4.000000000000003 6 (5.50935717240673e-15-1.3322676295501878e-15j) 5.6681525640985315e-15 7 (2.828427124746186+2.8284271247461925j) 3.9999999999999987
DC成分が含まれている場合、、例えば、 sin(x) + 2 の場合
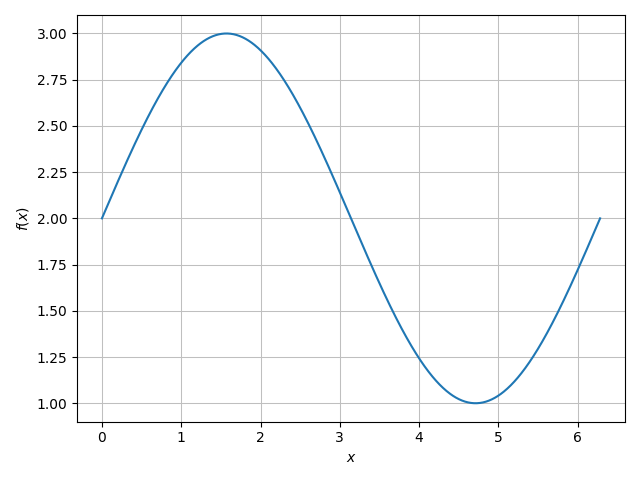
DFTの結果は以下、DC成分を示すk=0の出力が16になっている
*** DFT output *** 0 (16+0j) 16.0 1 (-7.771561172376096e-16-4j) 4.0 2 (-5.541681397207245e-16-6.661338147750939e-16j) 8.665082724754263e-16 3 (-3.3306690738754696e-16+9.992007221626409e-16j) 1.0532500405730103e-15 4 (2.220446049250313e-16-7.768113139884291e-16j) 8.07923031059731e-16 5 (-2.7755575615628914e-15-6.661338147750939e-16j) 2.8543745438774784e-15 6 (-3.1876482493291672e-15-2.220446049250313e-16j) 3.1953724615492976e-15 7 (3.6637359812630166e-15+4.000000000000002j) 4.000000000000002
周期が整数倍ではなかった場合(計測範囲が周期からずれている場合) sin(1.5x)で1.5周期計測してしまった場合

DFTを計算すると、DC成分、1倍成分、2倍成分が検知されている。
*** DFT output *** 0 (1.414213562373095+0j) 1.414213562373095 1 (2.707106781186547-0.2928932188134523j) 2.722905353179411 2 (-2.4142135623730954+0.9999999999999998j) 2.613125929752753 3 (-0.7071067811865462-0.29289321881345254j) 0.7653668647301783 4 (-0.585786437626905-3.0796421157949656e-16j) 0.585786437626905 5 (-0.7071067811865479+0.29289321881345154j) 0.7653668647301796 6 (-2.4142135623730936-1.0000000000000022j) 2.6131259297527527 7 (2.707106781186549+0.29289321881345765j) 2.722905353179413
証明すっ飛ばしてサンプルコードを書いた。細かい理屈は追いつかないけど、まぁ挙動は分かった。この実装だと愚直に同じ計算を何度も行っているため、サンプル数が大きくなると実行時間が問題になる(サンプル数8の場合、8x8で64回)。再計算を削減するためFFTを使うことになるのだろう(多分)
■参考資料
How to implement the discrete Fourier transform
https://www.robots.ox.ac.uk/~sjrob/Teaching/SP/l7.pdf